Вектор

Величины, которые кроме скалярного значения имеют направление, называются векторами. Другими словами, любая упорядоченная пара точек (А и В) задают направленный отрезок или вектор АВ. Термин "вектор" (от лат. vector - переноситель) ввел Гамильтон в 1848 году. Сейчас их изучают в школе, но вся векторная алгебра (теоретически) и физика (практически) связаны с векторами. В данной статье даются основы векторов с математической и программерской точки зрения.

Что такое вектор? Посмотрим на рисунок:

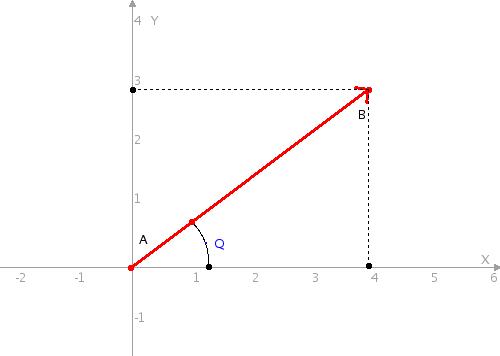
Здесь должен был быть расунок. Украли :-)
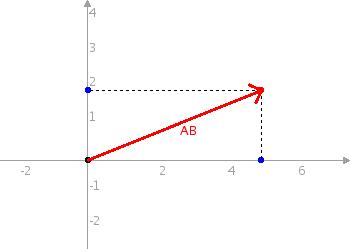
Рис. 1 Вектор АВ

Нормальный вектор :-) Еще одно достоинство векторов: начальная точка А может быть поставлена не в начало координат, а в любое место плоскости XY. Почему достоинство? Поясню: если бы так не было (т.е. каждая точка имела координаты), то наш вектор обозначался бы 4-мя цифрами, а на самом деле координат только две. Теперь о знаке. Если нужно чтобы вектор АВ принял противоположный знак нужно просто нарисовать вектор в противоположную сторону, как показано на рисунке 2.

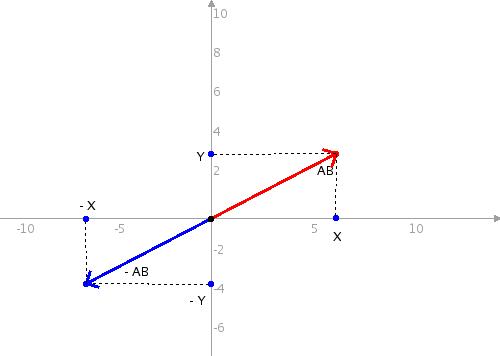
Тут должен был быть рисунок. Украли :-)
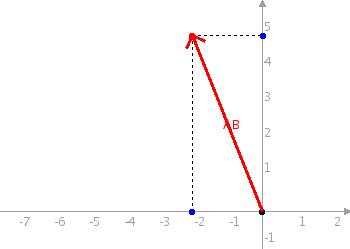
Рис. 2 Вектор АВ и противоположный ему


Длина (или модуль) находится как корень квадратный из сумы квадратов векторных координат. Формула:

A-a-a!

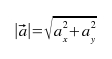
На С++ функция нахождения длинны такая:

#define d double

d vec_length(d x, d y)
{

return pow((pow(x,2)+pow(y,2)),0.5);

}


Многие знают, как складывать и вычитать векторы, как множить их на константу и.т.д. Но еще можно их вращать около центра координат, переносить конец векторов в любую точку плоскости и, скомбинировав все сказанное - вращать их вокруг заданной точки.

На С++ приведены примеры вращения вокруг начала координат:

#include <math.h>
#define d double

struct l2vektor
{

d x;
d y;

}

int main()
{

d ang = M_PI/2;

l2vektor a,b;

a.x=5; a.y=2; // вектор а(5,2); рис. 3

b.x=a.x*cos(ang)+a.y*sin(ang);
b.y=a.y*cos(ang)-a.x*sin(ang);
/*после выполнения этого кода: b(-2,5); рис. 4

}

 

A-a-a!
Рис. 3 Вектор АВ до вращения

A-a-a!
Рис. 4 Вектор АВ после вращения

 

Вращение конечной точки вокруг заданной - дело, по сути, простое. Пожалуйста:

#include "lvektor.h"
#include <math.h>

l2vektor rot_vek(l2vektor o, double ax, double ay, double ang)
{

l2vektor a;

a.x = o.x - ax;
a.y = o.y - ay;

double x, y;

x = a.x*cos(ang)+a.y*sin(ang);
y = a.y*cos(ang)-a.x*sin(ang);

a.x = x + ax;
a.y = y + ay;

return a;

}


Все объясняет рисунок 5

A-a-a!

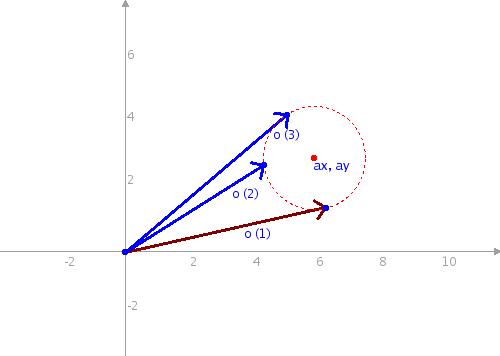
Рис. 5 Вектор о участвует во вращении вокруг точки

"Родной" вектор о (1) будучи, повернут на какой-то угол ang вокруг точки, имеющей координаты ax, ay перешел в "не родной" вектор о (2).

Тримерный вектор от нашего отличается только тем, что находится в пространстве и имеет одну дополнительную координату z.

A-a-a!
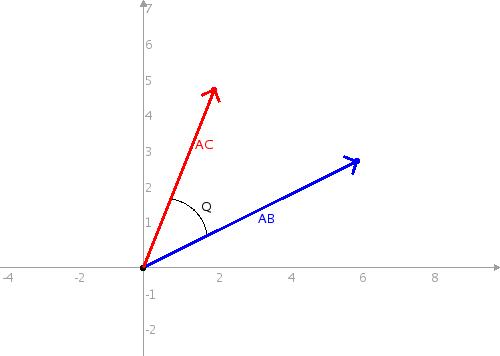
Рис. 6 Угол между векторами

Теперь перейдем к углу между векторами (как видно из рисунка этот угол - Q). Эта формула определяется отношением скалярного произведения к произведению модулей (длин) векторов:

A-a-a!

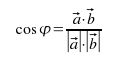
На С++:

#include <math.h>

double scal_vek(l2vektor a, l2vektor b)
double abs_vektor(l2vektor a)

double ang_mvek(l2vektor a, l2vektor b)
{

return acos(scal_vek(a,b)/(abs_vektor(a)*abs_vektor(b)));

}

double scal_vek(l2vektor a, l2vektor b)
{

return a.x*b.x + a.y*b.y;

}

double abs_vektor(l2vektor a)
{

return pow((pow(a.x,2)+pow(a.y,2)),(0.5));

}


Если хотите, скачайте модуль для С/С++ (тут для Windows) (тут для Linux). Там Вы найдете дву- и трехмерные векторы, направляющие косинусы пространственных векторов и.т.д. А (тут для Windows) (тут для Linux) Вы найдете расширенный "векторный" модуль, в котором представлены функции вращения векторов вокруг заданной точки.

На этом разрешите закончить и откланятся.

НАЗАД

Hosted by uCoz