Пишем выполнитель математических виражений

Пишем выполнитель математических выражений

Sin или не sin? Вот в чем вопрос...
("sin" в смысле не "грех" а в смысле "синус" :-)

Итак, мы будем писАть выполнитель математических виражений. Что для этого нужно? Любой язык, поддерживающий метод рекурентности (использование функцией самой себя). Любой из современных языков поддерживает этот метод (Delphi, C++Builer, Kylix, .NET).

Нам понадобится функция:
float expm(char s[], float par); // С++
function expm(s:string; par:extended):extented; // Delphi или Kylix

Ну, к примеру нам надо решить условие sin(x) с переданным нам параметром 0. Итак, опишу вам алгоритм:

1. Спросить, sin на первом месте?
    Если да:
    1.1. Убрать из условия "sin(" и относящуюся к синусу ")".
    1.2. Записать результат sin с заданным аргументом expm([новое условие], par).
       // параметр par везде один и тот же
    Если нет:
    1.3. Спросить, x на первом месте?
       Если да:
       1.3.1. Записать par в результат.
       Если нет, то принудительно закончить функцию.

Такая функция может решать sin(x), sin(sin(x)), sin(sin(...n(sin)(x)...)). Теперь добавим cos.

1. Спросить, sin на первом месте?
    Если да:
    1.1. Убрать из условия "sin(" и относящуюся к синусу ")".
    1.2. Записать результат sin с заданным аргументом expm([новое условие], par).
       // параметр par везде один и тот же
    Если нет:
    1.3. Спросить, con на первом месте?
        Если да:
        1.3.1. Убрать из условия "con(" и относящуюся к косинусу ")".
        1.3.2. Записать результат cos с заданным аргументом expm([новое условие], par).
Если нет:
          1.3. Спросить, x на первом месте?
      Если да:
          1.3.1. Записать par в результат.
          Если нет, то принудительно закончить функцию.

А вот данная функция может решать sin(x), cos(x), sin(cos(x)), cos(sin(x)), sin(...n(sin||cos)(x)...), cos(...n(sin||cos)(x)...). Надеюсь, смысл алгоритма понятен. А Вы можете добавить tg, cth, (sh, ch, th, cth - гиперболические тригонометрические функции), возведение в любую степень (для тех, кто еще не знает: a^b = exp(b*ln(a)) ), и так далее. Это все простые функции, а ведь Вы сможете добавить более сложные.

Это еще не все :-)

Хоть функция и решает выражения n-ой вложенности, но она выдаст ошибку на простейшей функции: x+x или x/x или x*x или x-x. Она выдаст ошибку и при решении более сложного выражения: (cos(sin(x)))+(tg(x)). Я взял cos(sin(x)) и tg(x) в скобки, чтобы Вам было удобнее. Можно и без них. Наш предыдущий алгоритм годится только на то, чтобы решать одночлены. Многочлены он решать не способен. Вот новый алгоритм:

1. Задать цикл от i=1 до количества одночленов. // поясню на примере
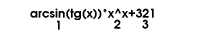
Формула
    // обозначенное цифрами - одночлены, а все вместе - многочлен.
    1.1. Решить i-тый одночлен.
    1.2. Результат записать и (+, -, *, / - зависит от выражения) на...
Повторить цикл
2. Записать результат многочлена и выйти из функции.

Вот и все! Дерзайте!