Метод жордановых преобразований i-нуль-таблиц для решения систем линейный уравнений

Здравствуйте! Сегодня у нас пойдет речь об одном из методов решения систем линейных уравнений. Да, знаю: в школе нас учат методу подстановки, сумы и разницы элементов, в университете: методам Крамера и Гаусса (довольно сложно для программирования). Но ни в школе и в универе (на Украине) нас не учат этому способу, хотя он очень удобен не столько для кодинга, сколько для математики. Это метод абсолютно безразличный к числу переменных и уравнений - все равно он выдает правильный ответ (если, конечно, его, верно, решить :-) Итак, в чем он состоит?

1. Записывается система уравнений

2. Преобразовываете ее так, чтобы после знака равно был ноль

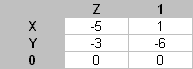
3. Записывается нуль-таблица (рис. 1)

Рис. 1

Суть алгоритма заключается в том, чтобы все переменные и ноли поменять местами. Делается это так:

4. Выбирается любая переменная (кроме столбика с названием "1") (обычно я начинаю из левой стороны - на решение это никак не влияет)

5. Также выбирается из того столбика любое число, окромя 0 (нам придется на него делить) - желательно чтобы это была единица. Это - главный элемент.

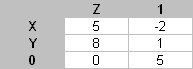
6. Меняется переменная и нуль местами (рис. 2)

7. В столбце, содержащем главный элемент, оставляется все, как есть, в противном случае Вы переходите к пункту 8

8. В строке, содержащей главный элемент, меняется знаки на противоположные. В противном случае Вы переходите к пункту 9

9. Все остальные поля решаются с помощью правила "прямоугольника"

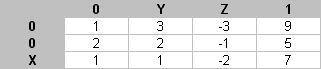
Рис. 2

Правило прямоугольника: в квадрате данного элемента с главным элементом есть главная диагональ и вторичная диагональ. Вычисляется очень просто: Вы из произведения главных элементов вычитаете произведение вторичных.

10. Все числа делятся на главный элемент (даже главный элемент Вы должны поделить на самого себя)

11. Вычеркивается столбец, содержащий главный элемент

12. Если еще есть переменные в названиях столбиков и есть ноли в названиях строк, Вы переходите к пункту 4. Если нет - выходите из алгоритма

Строки - это уравнения. Если "в названии" стоит 0, то можно уравнение сократить (рис. 3).

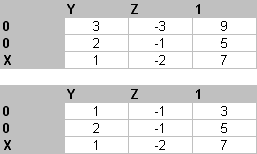
Рис. 3

Вашему вниманию представляется полное решение системы, состоящей из 3 уравнений с 3-мя переменными:

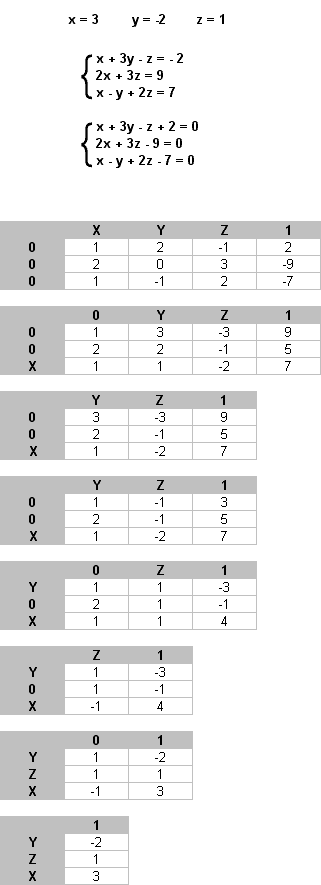
Рис. 4.

Тут могут быть три случая:

1. Система имеет одно решение (рис. 4)

2. Система имеет их множество (рис. 5)

3. Система не имеет ни одного решения (рис. 6)

Рис. 5

Рис. 6

Результат:

X = -5Z + 1

Y = -3Z - 6
Z принадлежит R

Тут, в третьем уравнении, 0 = 0 + 5, т.е. 0 = 5 что неверно

Для программиста (в теории :-) блок-схема выглядит так:

Тут должна была быть блок-схема!

Рис. 7

Но только в теории - на практике ничего не выйдет. А чтобы вышло, надо чтобы на месте блока "1" выполнялись следующие условия:

· Надо чтобы в таблице на месте выбираемого элемента был не ноль

· Места уже "поменянных" элементов тоже не следует

Почему я не ввел эти элементы в блок-схему? Все очень просто: я ведь не знаю, какую таблицу Вы будете использовать (а может и не таблицу вовсе - тут может, сгодится динамический массив). Да, я знаю, блок-схема с "похожестью на С" :-) (я писал программу на Borland C++Builder 6.0) - это сделано только для того, чтобы уменьшить размеры.

Вот и все, что хотелось сказать. Надеюсь министерство образования Украины введет этот способ в программу ВУЗов. Сайонара!