Нахождение детерминанта матрицы
Добрий день, панове! Речь у нас пойдет об определителях (детерминантах) матриц. Зачем он нужен? Отвечаю: нахождение обратной матрицы, развязывание систем линейных уравнений методом Крамера, нахождение ранга матрицы - все это основано на определении детерминанта матрицы.
Мы (люди) редко находим определители матриц свыше пятого порядка, ведь это уйма работы! Для примера, мы находим матрицу 3-го порядка. Я высчитываю 3 детерминанта матриц 2-го порядка (миноры), умножаю их на те элементы, которые я вычеркнул, и, не забывая про знаки, складываю их. Нам помогает использование свойств определителей, но при нахождении детерминанта матрицы выше 5-го порядка оно только мешает. Что же делать?
Ответ прост: загрузить компьютер :-). Приведенный ниже алгоритм может находить детерминанты матриц n-го порядка (только бы памяти хватило :-). Алгоритм (сравнительно) большой, поэтому я буду приводить его по частям.
Сначала "сердце" алгоритма - метод выделения из большей матрицы нескольких меньших матриц. Приведу блок-схему:

Рис. 1
Поначалу немного запутанно, но если вдуматься, все выходит верно. Для нежелающих копаться в блоках привожу С++ код:
for(int d=0;d<n;d++) // задаем цикл: эти элементы будем вычеркивать
{
for(int j=0;j<n;j++) // задаем цикл: это строки матрицы
{
for(int k=0;k<n;k++) // задаем цикл: это столбцы матрицы
{
if(k!=d) // проверяем: не этот столбец мы вычеркнули
{
if(j!=0) // проверяем: не эту строку мы вычеркнули
{
if(!bo) B[j-1][k] = A[j][k]; else B[j-1][k-1] = A[j][k]; // проверяем: до или после столбца, который мы вычеркнули
}
}
else bo = true;
}
bo = false;
}
for(int i=0;i<(n-1);i++)
{
for(int j=0;j<(n-1);j++)
{
cout << B[i][j] << " "; // выводим этот элемент матрицы
}
cout << endl;
}
cout << endl;
}
Не забудьте включить iostream.h в ваши модули. Использовать мы будем динамические массивы, так что если вы не знаете о них, добро пожаловать сюда. Напомню, что дин. массив, который отвечает 3-го порядка, задается так:
int n = 3;
float **A = new float*[n];
for(int i=0;i<n;i++) A[i] = new float[n];
Блок-схема самого алгоритма (функция det_mat):
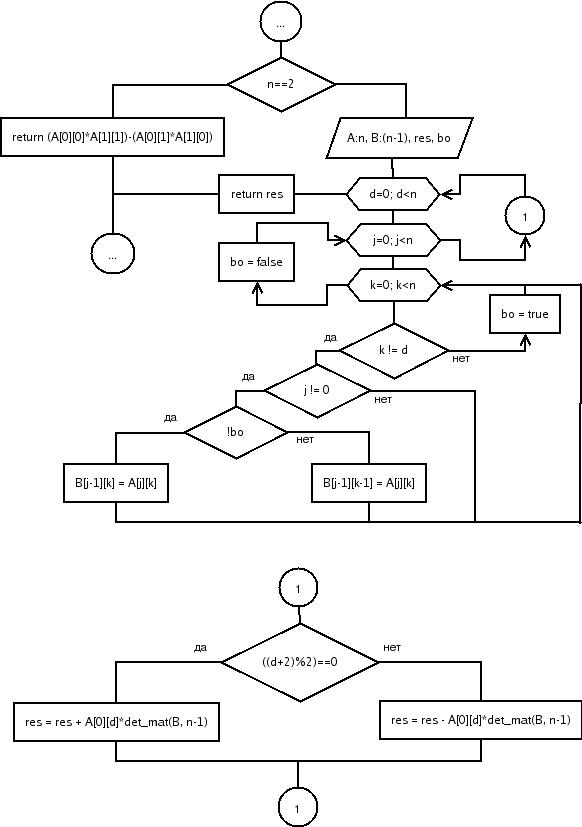
Рис. 2
А теперь код функции det_mat:
#include
<iostream.h> //
включаем
модуль, чтобы
cout
распознавался
корректно
float det_mat(float* M[], int n) // я
задаю не саму
матрицу, а
ссылку на нее
(*M[]) и порядок n
{
if(n==2) //
если n = 2, то
функция
возвращает
определитель
2-го порядка,
путем
вычитания
побочной диагонали
из главной
{
float s = (M[0][0]*M[1][1])-(M[1][0]*M[0][1]);
return s;
}
else // а
если n>2
{
float res = 0;
bool bo = false;
float **A = new float*[n]; //
объявляем
матрицу n-го
порядка
for(int i=0;i<n;i++) A[i] = new
float[n];
for(int i=0;i<n;i++)for(int
j=0;j<n;j++)A[i][j]=M[i][j]; //
"наполняем"
матрицу A из
ссылки M
float **B = new float*[n-1]; //
объявляем
матрицу (n-1)-го
порядка
for(int i=0;i<(n-1);i++) B[i] =
new float[n-1];
for(int d=0;d<n;d++) // задаем
цикл: эти
элементы
будем
вычеркивать
{
for(int
j=0;j<n;j++) //
задаем цикл:
это строки
матрицы
{
for(int k=0;k<n;k++) //
задаем цикл:
это столбцы
матрицы
{
if(k!=d) //
проверяем: не
этот столбец
мы
вычеркнули
{
if(j!=0) //
проверяем: не
эту строку мы
вычеркнули
{
if(!bo) B[j-1][k] = A[j][k]; else B[j-1][k-1] = A[j][k]; // проверяем:
до или после
столбца,
который мы
вычеркнули
}
}
else bo = true;
}
bo = false;
}
if(((d+2)%2)==0) res += A[0][d]*det_mat(B,n-1); else res -=
A[0][d]*det_mat(B,n-1); // а
теперь знаки;
если сумма
строк и
столбцов
вычеркнутого
знака четна,
то мы
складываем
произведение
выч. цифры с
рекуррентным
значением
этой же
функции, но
на единицу меньшей
матрицы, если
нет - то
вычитаем.
}
return res;
}
}
Определитель можно вычислять только для квадратной матрицы, т.е. количество строк должно быть равно количеству столбиков. Неквадратная матрица детерминанта не имеет.
Теперь о памяти. Все зависит от того, детерминант матрицы какого порядка вы будете вычислять. К примеру, 3-й порядок, вызвал 4 запуска этой функции. И в каждой от 10 до 120 байт информации. 4-го порядка - уже 17 запусков этой функции, в каждой из которых от 10 до 210 байт, т.е. больше килобайта. Имейте это в виду.
Если Вы будете использовать этот алгоритм на практике, прошу скачать модуль. Тут для Linux, тут для Windows.